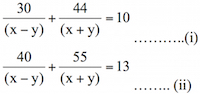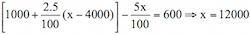learn icon

Learning Home
L&T ECC3i InfotechABBAccentureAdobeAgilentAkamaiAmazonAmdocsAricent More 

Sample Aptitude Questions of L&T ECC

A quick review on sample aptitude question
Rate Us
Views:37808
Instant Access to Free Material
  1. The work done by a woman in 8 hours is equal to the work done by a man in 6 hours and by a boy in 12 hours. If working 6 hours per day 9 men can complete a work in 6 days, then in how many days can 12 men, 12 women and 12 boys together finish the same working 8 hours per day?
    1. 21⁄2 days
    2. 11⁄2 days
    3. 31⁄2 days
    4. None of these.
    Answer: Option B
    Given: 8 women = 6 Men = 12 Boys
    ∴ 12 Men + 12 Women + 12 Boys
    = 12 Men + 9 Men + 6 Men = 27 Men
    We have, M1 = 9, D1= 6, t1 = 6, W1 = 1
    M2 = 27, D2 = ?, t2 = 8, W2 = 1
    ∴ M1D1T1W2 = M2D2T2W1
    ⇒ 9 × 6 × 6 × 1 = 27 × D2 × 8 × 1
    => D2 = 3/2 days or, 11⁄2.
    .
  2. At the start of a seminar, the ratio of the number of male participants to the number of female participants was 3 : 1. During the tea break, 16 participants left and 6 more female participants registered. The ratio of the male to the female participants became 2:1. The total number of participants at the start of the seminar was -
    1. 64
    2. 48
    3. 54
    4. Data Insufficient.
    Answer: Option D.
    In this question, as per the information given we cannot determine how many are males and how many are females out of 16 participants who left. So, data is insufficient to answer the given question.
  1. A man can row 30 km upstream and 44 km downstream in 10 hours. Also, he can row 40 km upstream and 55 km downstream in 13 hours. The rate of the current is -
    1. 3 km/hr
    2. 3.5 km/hr
    3. 4 km/hr
    4. 4.5 km/hr
    Answer: Option A.
    Let the speed of the man in still water be x km/hr and speed of the stream be y km/h then

    Solving (i) and (ii) x = 8 km/hr and y = 3 km/hr
    So the rate of stream is 3km/hr.
  2. There are two identical vessels, X and Y. Y is filled with water to the brim and X is empty. There are two pails A and B, such that B can hold half as much water as A. One operation is said to be executed when water is transferred from Y to X using A once and water is transferred to Y from X using B once. If A can hold a liter of water and it takes 40 operations to equate the water level in X and Y, what is the total volume of water in the system
    1. 10 liters
    2. 20 liters
    3. 40 liters
    4. 203⁄4 liters
    Answer: Option C.
    In one complete operation, water transferred = 1 - (1/2) = 1/2 liters as 1 liter goes from Y to X. So 1 liter is contained in X. But ½ liter goes from X to Y as well. So net ½ liters remain in X. If it takes 40 operations to equate water level,
    ∴ 40 × (1/2) = 20 liters is contained in X and Y.
    Hence total volume of water in the system is 40 litres. Hence, 3rd option.
  3. A salesman's terms were changed from a flat commission of 5% on all his sales to a fixed salary of Rs. 1,000 plus 2.5 % commission on all sales exceeding Rs. 4,000. If his remuneration as per the new scheme was Rs. 600 more than by the first scheme, what were his sales worth
    1. Rs. 11, 000
    2. Rs. 17, 000
    3. Rs. 16, 000
    4. Rs. 12, 000
    Answer: Option D.
    Let his sales were worth Rs. x.
    So as per the question,

    So answer is D option.
    Mphasis Preparation Links
  4. In a class with a certain number of students if one student weighing 50 kg is added then the average weight of the class increases by 1 kg. If one more student weighing 50 kg is added then the average weight of the class increases by 1.5 kg over the original average. What is the original average weight (in kg) of the class?
    1. 46
    2. 4
    3. 2
    4. 47
    Answer: Option D.
    Let x  be the original average and n be the number of students. Let  x1, x2,  x3 ,. . . .. xn  be the weights of n students respectively. Therefore,
    x1, x2,  x3 ,. . . .. xn  / n = x
    x1, x2,  x3 ,. . . .. xn   =  nx...............(1)
    Now,according to 1st condition we have 
    x1, x2,  x3 ,. . . .. xn  + 50/ n+1 =  x+1
    x1, x2,  x3 ,. . . .. xn   =  (n+1)(x+1) - 50..............(2)
    Further,according to 2nd condition we have
     x1, x2,  x3 ,. . . .. xn  + 50+50/ n+2 =  x+1.5
    x1, x2,  x3 ,. . . .. xn   =  (n+2)(x+1.5) - 100..............(3)
    Solving (1) and (2), we get
    x + n = 49…………….. (4)
    Solving (1) and (3), we get
    4x + 3n = 194  ……………. (5)
    Now, Solving (4) and (5), we get
    n = 2, x = 47
    So, the original average weight (in kg) of the class = 47
    Alternate Solution :
    Let x be the original average and n be the number of students.
    From the first increase in the average,
    we get 50 – x = n + 1
    From the second increase in the average,
    we get 100 – 2x = 1.5 (n + 2)
    Solving, we get the value of x = 47.
  5. The average marks of a student in 8 subjects is 87. Of these, the highest marks are 2 more than the one next in value. If these two subjects are eliminated, the average marks of the remaining subjects are 85. What are the highest marks obtained by him
    1. 94
    2. 91
    3. 89
    4. 96
    Answer: Option A.
    Let highest marks be (x +2), So, next score = x Total of 8 subjects = 8 × 87 = 696
    So, As per question, 696 - x = (x+2) / 6 =85
    ⇒ x = 92 So, highest marks = (x + 2) = 92 + 2 = 94.
  6. If a bucket is 80% full, then it contains 2 liters more water than when it is 662/3% full. What is the capacity of the bucket?
    1. 10 liters
    2. 15 liters
    3. 162/3 liters
    4. 20 liters
    Answer: Option B.
    Let the capacity of bucket is x litre.
    As per the question,
    we have [(4x)/5 - (2x)/3] = 2
    ⇒ x = 15 litres.
  7. The electricity bill of a certain establishment is partly fixed and partly varies as the number of units of electricity consumed. When in a certain month 540 units are consumed, the bill is Rs. 1,800. In another month 620 units are consumed and the bill is Rs. 2,040. In yet another month 500 units are consumed. The bill for that month would be
    1. Rs. 1,560
    2. Rs. 1,680
    3. Rs. 1,840
    4. Rs. 1,950
    Answer: Option B.
    Let V be the variable part of the bill and F be the fixed part. Given 540V + F = 1800 & 620 V + F = 2040. Solving these we get V = 3 and F = 180. So when 500 units are consumed, 500V + F = 500 × 3 + 180 = Rs. 1680.
  8. Two cyclists start on a circular track from a given point but in opposite directions with speeds of 7 m/sec and 8 m/sec respectively. If the circumference of the circle is 300 metres, after what time will they meet at the starting point for the first time
    1. 20 sec
    2. 100 sec
    3. 300 sec
    4. 200 sec
    Answer: Option C.
    S = D/T The times taken by the two cyclists to reach the starting point are 300/7 seconds and 300/8 seconds respectively. So, they will meet at the starting point after LCM(300/7, 300/8) = 300 seconds.
Campus Placement ad
Rate Us
Views:37808

Most Popular Articles - PS

Placement Papers of all major companies

Placement Papers of all major companies
List of IT Companies

List of IT Companies
Aptitude Questions of all major companies

Aptitude Questions of all Major Companies
Test Pattern of all major companies

Test Pattern of all major companies
Technical Questions of all major companies

Technical Questions of all major companies
List of Core Companies

List of Core Companies
Interview Questions of all major companies

Interview Questions of all major companies
All About GATE Entrance Exam

All About GATE Entrance Exam

How to prepare for Aptitude Tests?

GATE Previous Year Papers

GATE Previous Year Papers